Today, I've just got a follow-up on my earlier post regarding the CrossFit Games scoring system ("Opening Pandora's Box: Do We Need a New Scoring System"). In fact, this is actually a follow-up to a comment to that post.
Tony Budding of CrossFit HQ was kind enough to stop by and respond to my article, in particular my suggestion that we move to a standard deviation scoring system. You can read my post and Tony's comment in full to get the details, but the long and short of it is this: HQ is sticking with the points-per-place system for the time being. I'd like to keep the discussion going in the future about possibly moving away from this system, but for now, I accept that the points-per-place is here to stay. Tony made some good points, and I understand the rationale, though I stand by my argument.
Anyway... Tony mentioned that they are still working on ways to refine the system. Certain flaws, like the logjams that occurred at certain scores (like a score of 60 on WOD 12.2) are probably fixable with different programming, and there are some tweaks that could be made to address other concerns (for instance, only allowing scores from athletes who compete in all workouts). But I had another thought that would allow us to stick with the points-per-place system while gaining some of the advantages of a standard deviation system.
At the Games for the past two years, the points-per-place has been modified to award points in descending order based on place, with the high score winning (in contrast to the open and regionals, where the actual ranking is added up and the low score wins). In addition, the Games scoring system has wider gaps between places toward the top of the leaderboard. In my opinion, this is an improvement over the traditional points-per-place system because it gives more weight to the elite performances. However, I think we can do a little better.
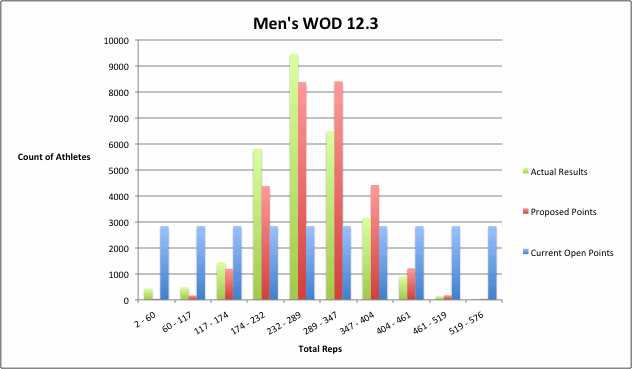
First, here is my rationale for why we should have wider gaps between the top places. If you look at how the actual results of most workouts are distributed, you'll see the performance gaps are indeed wider at the top end. The graph below is a histogram of results from Men's Open WOD 12.3 last year:
There are fewer athletes at the top end than there are in the middle, so it makes sense to reward each successive place with a wider point gap. However, the same thing occurs on the low end, with the scores being more and more spread out. But the current Games scoring table does not reflect this - the gaps get smaller and smaller the further down the leaderboard you go (the current Open scoring system obviously has equal gaps throughout the entire leaderboard).
Now, another issue with the current Games scoring table is that it's set up to handle only one size of competition (the maximum it could handle is around 60). So let's try to set up a scoring table that will address my concern about the distribution of scores but can be used for a comeptition of any size (even the Open).
Obviously, the pure points-per-place system used in the Open will work on a competition of any size, but what is essentially does is assume we have a uniform distribution of scores. Basically, the point spread between any two places is the same regardless of where you fall in the spectrum. So what happens is the point difference between 100 burpees and 105 burpees becomes much wider than the gap between 50 and 55 or 140 and 145. So my suggestion is this: let's use a scoring table that ranges from 0-100 but reflects a normal (bell-shaped) distribution rather than a uniform (flat) distribution. The graph below shows that same histogram of WOD 12.3 (green), along with a histogram of my suggested scores (red) and a histogram of the current open points (blue). The scale is different on each histogram, but there are 10 even intervals for each, so you can focus on how the shapes line up.
You can see that the points awarded with the proposed system are much more closely aligned with the actual performances than the current system. And this was done without using the actual performances themselves - I just assumed the distribution of performances was normal and awarded points, based on rank, to fit the assumed distribution.
Now, you may be asking, how well does this distribution fare when we limit the field to only the elite athletes? Well, the shape does not tend to match up as well as we saw in the graph above. Part of this is due to the field simply being smaller, so there is naturally more opportunity for variance from the expected distribution. However, for almost every event in last year's Games, there is no question that the normal distribution is a better fit than the current Games scoring table. The chart below shows a histogram the actual results from the men's Track Triplet along with the distribution of scores using the proposed scoring table and the current scoring table. I have displayed the distribution of scores from the scoring table with lines rather than bars to make the various shapes easier to discern.
As stated above, we do not perfectly match the actual distribution of results. But clearly the actual results are better modeled with the normal distribution than with the current scoring table. As further evidence, the R-squared between the actual results and the proposed scoring table is 96.0%; the R-squared between the actual results and the current scoring table is only 83.9%. If we make this same comparison for each of the first 10 events for men and women (excluding the obstacle course, which was a bracket-style tournament), the R-squared was higher with the proposed scoring table than with the current table, with the exception of the women's Medball-HSPU workout.
I believe this proposed system, while not radically different than our current system, would be an improvement but would not have any of the same issues that concerned HQ about the standard deviation system. While the math used to set up the scoring system may be difficult for many to digest, that's all done behind the scenes and the resulting table is no more difficult to understand than the current Games scoring table, especially if we round all scores to the nearest whole number. If used in the Open, we'd almost certainly have to go out to a couple decimal places, but I think otherwise this system would work fine. And since we are still basing the scores on the placement and not the actual performance, this system also does not allow, as Tony said, "outliers in a single event [to] benefit tremendously." It does, however, reward performances at the top end (and punish performances at the low end) more than the current system.
I appreciate the fact that Tony took the time to review my prior work, and I hope that he and HQ will consider what I've proposed here.
*Below is the actual table (with rounding) that would be used in a field of 45 people (men's Games this year), compared with the current system.
**MATH NOTE: In case you were wondering, here is the actual formula I used in Excel to generate the table:
POINTS = normsinv(1 - (placement / total athletes) + (0.5 / total athletes)) * (50 / normsinv(1 - (0.5 / total athletes)) + 50
This first part gives us the expected number of standard deviations from the mean, given the athlete's rank. Next we multiply that by 50 and divide by the expected number of standard deviations from the mean for the winner (this will give the winner 50 points and last place -50 points). Then we add 50 to make our scale go from 0-100.



Hi Anders,
ReplyDeleteI have been trying to reproduce exactly your table in excel. I get 164 points for the winner instead of 100. We are designing a competition and would like to try your formula. Could you please post exactly the excel forumala so that I can copy and paste it?
Euan,
ReplyDeleteThanks for giving this method a shot. Be sure to let me know how it works out for you. I'm guessing you may have had a parenthesis in the wrong spot when you converted the formula to Excel. Anyway, here is one way to do it in Excel:
In column A, starting on row 1, make a list of places from 1st through last in ascending order. Make sure not to have anything else in column A.
In cell B1, use the following formula:
=NORMSINV(1-(A1/MAX(A:A))+(0.5/MAX(A:A)))*(50/NORMSINV(1-0.5/MAX(A:A)))+50
Copy that formula down in column B to the end of your list of places.
If you have a field of 20 athletes, the points should look be 100 for 1st, 87 for 2nd, 79 for 3rd,... 21 for 18th, 13 for 19th, 0 for 20th.
If you're still having trouble, send me an email (anders@alumni.wfu.edu) and I'll send you an actual spreadsheet.
Anders, thank you for that it helps. The issue of course is to know exactly how many athletes you have competing before the start of the event. We have about 25 men and 10 women.
DeleteWe have a cut off (top 10) for the final event, how would we score that? using a different distribution of points per place or stick with the initial top 25 points version.
Some events will also have a different weighting, worth 50 points instead of 100. Should I divide the weighting of your formula by two for those?
WODcast will be running our scoreboard so I can't adjust point distribution through the day.
Hmm... some of this is just a matter of opinion I think. After the cut, do you want to give people a chance to make up a lot of ground? If so, then you'd want to reset the table after the cuts so that it will again go from 0-100. That way, a person could theoretically make up 100 points on someone else in that last event. However, if you feel like you want reward the top athletes more for their earlier performances, then maybe keep the old table, that way they can't lose as much ground in the last event. Cuts are just tricky to handle no matter what scoring system you use.
DeleteAs far as weighting events differently, the easiest way to do it is to create your initial 100-point table, then if you want to make an event worth a max of 50 points, just reference your original table and multiply all the values by 0.5. Does that make sense? That way you don't need to modify that original formula at all.
If you're having some issues with it, shoot me an email with some detail about the number of competitors, the weighting for the events, and how you want to handle the cuts. I can build out the tables you'd need pretty easily.
This is awesome work. Knowing how much Greg Glassman and company love to talk about the standard bell curve, I am hopeful that they'll go for this scoring system in lieu of the current one. Thanks for this.
ReplyDeleteI've implemented this method in my competition scoring system, but a question is what is the best way to handle ties with this method? Currently I assigned points for ties as the mean of the combined points for the tied places. So 1st and 2nd each get half of the combined points for 1st and 2nd. This keeps the total of points assigned in an event the same as if there were no ties. If I use the mean place for the tied places, i.e. 1.5 in the previous example, then the total of the points assigned via this method changes slightly.
ReplyDeleteInteresting question. Not sure there's a "right" answer, but I like the way you are doing it to average the points, not the placement. It's easier to handle and it keeps the total points unchanged, as you pointed out. Either way, much better than the current system awarding the highest possible place to all tied athletes.
ReplyDeleteHi Anders,
ReplyDeleteI'm a little late to this party, but I'm going to comment a bit on your thoughts here as well as in the original Pandora's Box post. The root of the disconnect between you and Tony is that you don't have the same goals. Flaw #2 in your original post is that there should be an award for outstanding performances. If that were fixed, then the direct consequence would be that it would punish the generalist and reward the specialist. But that is contrary to CrossFit's definition of fitness. Many of the real-world places where fitness matters are binary decisions. Do you kill the bad guy or does he kill you? Do you get your wall of sandbags built high enough before the water comes or not? Can you run down the purse snatcher or not? If you kill the bad guy because you're stronger than him, then it wouldn't have mattered if you had an 800 lb squat rather than your 650lb squat. I think you'll agree that there's no way CrossFit is going to change their definition of fitness, so this "flaw" is null and void from the get-go.
Next, I think flaw #3 is pretty closely related to flaw #2. Like I mentioned above, these binary questions are what matters. It's not so important whether a one-burpee increase in score improves your rank by 800 places or 300 places. And I think that if you fix this "flaw", then you're automatically going to be doing the wrong thing with respect to CrossFit's position on flaw #2. In short, if you reward people for the amount of spacing between contestants, then you're moving away from the binary aspects of fitness and thus towards rewarding specialists. Also, I think flaw #3 can be corrected with better programming, so it's not such an important question.
However, I do agree with you (and I think Tony would too) regarding flaws #1 and #4 (which are also closely related). For instance, consider a hypothetical scenario where towards the end of the games Dan Bailey was in 28th place and Mikko Salo was barely ahead of Rich Froning for first place. Now imagine a workout comes up which happens to play to Dan Bailey's strengths. In the middle of the workout, Dan is out front, but he sees that Rich is a little bit ahead of Mikko. Since Dan is close friends with Rich, he could slow down a bit...enough so that Rich could pass him but still remain ahead of Mikko. This action could conceivably change the outcome and make Rich win instead of Mikko. This is definitely a problem. I don't think this has happened yet, but with $250,000 at stake, you have to admit that if a situation arose, it would be very logical for Dan to throw the event so his buddy and training partner would get a big payday.
One way to deal with this problem would be to use condorcet voting. A system like this would mean that every event can be considered a vote in a race between every pair of athletes. You make a big table of all contestant pairings. If in event #1, athlete A beats athlete B, then that's essentially a vote that athlete A is fitter than athlete B. If in event #2, athlete B wins, then that's a vote that athlete B is fitter. The final voting resolution can be a bit complicated, but on the whole I think this seems like a really promising approach. The current ranking system is probably a little easier to understand, but I think a condorcet system would be very understandable. It would also have the side benefit of educating a lot of people about condorcet voting, which I think would be a good thing because it could also benefit the U.S. political system. :P (You know...just had to throw that in there...rest day discussions and all.)
I would love to do some research and analyze the results of past Games with this condorcet method to see how it would do, but unfortunately I don't have the time. I would be very interested if someone else posted an analysis like this.
MB,
DeleteThanks for your thoughts. I think your condorcet voting solution is an interesting one, although I doubt it would be seriously considered by HQ, considering it is not particularly easy for the casual fan to understand. Remember this was a major concern of Tony's regarding the standard deviation system.
I still believe that "outlier" performances should be rewarded to an extent. The argument that only placement matters in nature, which I've seen used in the past, isn't really rock-solid to me. In your example about killing the bad guy, that's true, you might not have needed the 800-lb. squat that time, but what about another "stronger" bad guy who you could not defeat without an 800-lb. squat? Or how about a situation where you need to move as many bags of food as you can - the more bags you move, the more food you have. If you're incredibly good at moving those bags of food, you get a great reward of more food. There's not always a clear demarcation of "strong enough" or "not strong enough."
And consider that what we consider an "outlier" performance is constantly evolving. In 2009, Aja Barto's 295-lb. snatch would have been just as good as 245-lb. snatch based on points-per-place. Today, a 245-lb. snatch would drop him down the rankings considerably. (Of course, the system I proposed on this post wouldn't fix that either, but then again that's why I titled it "IF we're going to stick with points-per-place...")
Anyway, it's all good discussion. I know everyone won't agree with my proposals, but I think we don't need to be content with the current system simply because that's what HQ is using.
Thanks for your thoughts.
You're probably right that the condorcet system's obscurity/difficulty might preclude it from consideration my HQ. But I think that it is easier for fans to understand than most (if not all) of your proposals because the condorcet system can be described in voting terms that people are already familiar with. The benefit of fixing flaws #1 and #4 might possibly outweigh the aspect of being harder to understand.
DeleteI understand the desire to reward outlier performances. I just think that if you're trying to do so, you have to explicitly address how your proposals avoid falling into the trap of rewarding specialists--because that is what HQ is concerned about. We want to make sure that the people who sacrifice endurance to achieve a bigger snatch are penalized more for the lack of endurance than they are rewarded for the bigger snatch.
I implemented the Concordet scoring system and looked at the results at the end of each workout. It doesn't change the top placements, but it is interesting. I'm pretty bad at making graphs so here's the raw data: https://docs.google.com/spreadsheet/ccc?key=0Ai8Zt3JFNCsmdFRxWko2LWMxZGl6dk5UX3R3VnVkZ1E
DeleteRon,
DeleteI'm a little unclear on how you made those calculations. It appears at first glance as though you are just using the rank on each event, but reversed (so first place is 45, second is 44, etc.). My understanding of the system MB suggested was that each athlete would have a FINAL score between 0-45, representing how many athletes he/she would have beaten in a head-to-head competition across all the events. Perhaps I'm not understanding it correctly.
By the way, just out of curiosity, I did re-score the Games using the system I proposed here. I did not re-scale the scoring table after the cuts, to be consistent with the Games, but I might consider doing that if I was in charge. The results were mostly the same as the originals. Some notable things:
-Men identical rankings 1-8.
-Holmberg moved to 9th and Ben Smith moved to 10th, with Mackay falling to 11th.
-Women identical 1-4.
-Camille moved to 5th, Akinwale to 6th, and Voboril dropped to 7th.
-Voigt moved to 9th and Valenzuela dropped to 10th.
So overall, we're talking about some minor shifts. Still, I think the theory behind the system I proposed makes it less arbitrary and gives it more credence than the current scoring table. Obviously, whether it's superior to other systems (like Condorcet voting) is up for debate.
OK, I had an incomplete implementation that basically just inverted places per points with proper tie scoring, so that's why there wasn't much change.
DeleteI rescored as follows: For each head to head matchup, for each WOD awards 1 pt to the winner, 1/2 points to each for a tie, with 1/2 of each of those for the skill WODs. Then compare the total WOD pts, with 1 to the winner and half to each in a tie. So each head to head matchup has 13.5 pts available. I believe this is Copeland's Method from the description on Wikipedia.
Kristan ends up 2nd, though she only beat 42 women (Annie and Talayna beat her). Talayna isn't 2nd though because Annie, Camille and Jenny Davis(!) beat her in head to head matchups.
Ron,
DeleteThat sounds more like what I was thinking. The results are definitely interesting, and it's an intriguing approach. Again, my main critique would be that it's going to be difficult for folks to understand how it works.
Good discussion going, though. I think one big takeaway is that over the course of 15 events, the scoring system doesn't make a huge impact. However, at the regional level (or in the Open), it can make a bigger difference because there aren't as many events to even things out. I'm not sure I have the time to do it anytime soon, but I'd imagine that implementing any of these different systems at any of the regionals would have really shifted things around a lot. It might be something I play around with during this year's Open though.
I really like learning and following your post as I find out them extremely useful and interesting. This post is in the same way useful as well as interesting . Thank you for information you been putting on developing your web page such an interesting. I offered something for my information. Point Sticks
ReplyDelete